HOME(EN) Company profile CB processing CHEMIFLEX Chemical treatment ATMag HOME(JP)
ATMag
Microstructural design of the heat-resistant Mg-Al-Zn-Ca-Sr alloys having balanced properties at ambient and elevated temperature
ATMag. Technical Data.
We hope that this article will help those, who use magnesium materials, to understand theoretical basis of the characteristics of magnesium materials known practically or experimentally.
Abstract
Effective elements of Ca and Sr were selected to improve heat resistance of AZ91 based magnesium alloys.
For die-casting, AZ91-1.0Ca0.5Sr alloy had well balanced tensile properties at ambient and elevated temperature. Crystal grain size was the deciding factor of tensile properties at ambient temperature. Factors of tensile properties at elevated temperature were studied using the constitutive equation to describe deformation at elevated temperature. The stacking fault energy of solid solution of aluminum and grain boundary coverage by metallic compounds of skeleton structure were most effective for strengthening at elevated temperature.
As the skeleton structure of die-cast material is broken into particles in extrusion processing, the strengthening mechanisms of the extruded material were studied. Grain refinement and solid solution of aluminum were the strengthening factors at ambient temperature. However at elevated temperature substantial decrease of the average distance between the metallic compounds of λ and increase of the threshold stress of σ0 were the factors accompanied by increase of grain boundary coverage of metallic compounds.
1. Design of the basic composition of the alloy having well-balanced tensile properties at ambient and elevated temperature
Magnesium materials are difficult to form by extrusion, rolling and forging due to its close-packed hexagonal crystal structure and, therefore the magnesium material for forming has not been provided and usually die-cast products have been used.
A lot of heat resistant magnesium alloys have been developed for die-casting, but these alloys sacrifice tensile properties at ambient temperature for improving properties at high temperature.
Introduction of magnesium forming materials is indispensable for expansion of magnesium market up to much larger aluminum materials and for this purpose design of new magnesium alloy composition is required.
We studied new alloys to respond these requirements and the outcome of the research will be discussed as bellow. Design of basic alloy composition having the balanced properties at elevated and ambient temperature will be discussed.
Design of the alloy by the first principles calculations
First Principles Calculations
A quantum mechanics, the first principle, based calculation method to not-empirically estimate physical mechanisms and properties using only atomic number for an input parameter, as the first principle is a fundamental law of materials in atomic and nanoscale region. It can calculate all energy and band structures of electrons in a model which consists of atomic number and atoms with known spatial coordinates.

Models for solid solution strengthening
At ambient temperature:
“Size effect” where movement of dislocation is hindered by misfit strain, a kind of lattice strain, attributed by the size difference between solute atoms and solution atoms.
At elevated temperature:
“Suzuki effect” which increases strength by fixed extended dislocations where solute atoms are segregated.
Stacking fault energy:
Energy needed to introduce a unit area of stacking fault, an interruption of the normal-stacking sequence of atomic planes in a crystal structure, into a perfect crystal.


↓
Width of extended dislocation: w
・Stacking fault energy is high. → w is narrower ⇒ Deformable
・Stacking fault energy is low. → w is wider ⇒ Difficult to deform

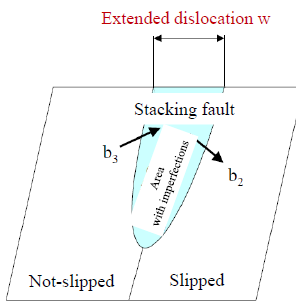
Stacking fault is a type of plane defect and characterized as the disordering of crystallographic planes or an interruption of the normal stacking sequence of atomic planes in a crystal structure. Stacking fault energy is defined as the energy required introducing the stacking faults per unit area in the perfect crystal. A schematic diagram of extended dislocation by stacking faults is shown in Fig 2. If the stacking fault energy, the energy required to introduce the stacking faults, is higher, it narrows the width w of the extended dislocations, where the dislocation is easily moved, and therefore deformation of the material is facilitated. In order to improve heat resistance of a material, the width w of the extended dislocation has to be wider or it is necessary to select an additional element for reducing the stacking fault energy. In Table 1, it shows the calculated value of the stacking fault energies of copper, aluminum and magnesium. Comparing with magnesium, copper and aluminum have larger stacking fault energy, so it is understood that they are easily deformed.
Effective elements for improvement of the heat resistance

Effective elements for decrease of SFE:In, Tl, Sc, Pb, Al, Y, Sn, BiTl, Pb, Bi Y, Sc, In
Tl,Pb,Bi →Hazardous Y,Sc,In → Rare metals, Expensive
↓
Notable element : Aluminum
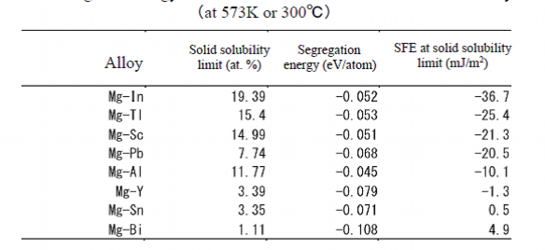
Table 2 shows the stacking fault energies of the elements added to magnesium at 300 deg. C. They were calculated by the first-principles calculation. As the concentration of the solute atom affects the stacking fault energy, it was calculated in a condition that added elements are dissolved in magnesium as solid solution up to their solubility limits. Yttrium, Y, has large segregation energy so as to solute atoms in Suzuki effect, but its solubility limit is small. As the stacking fault energy is affected by both factors, the stacking fault energy of yttrium is not large.As shown in Table 2, effective additive elements to magnesium are not many to decrease the stacking fault energy. In the limited elements harmful elements such as tellurium, Te, lead, Pb, and bismuth, Bi, cannot be commercially used. On the other hand the sources of rare metals of yttrium, scandium, Sc, and indium, In, are restricted, so they have risks in supply and a problem that their prices are expensive. Therefore, among the elements with larger solid solubility limit and smaller stacking fault energy, we focused on aluminum, Al, which is widely used.
Effect of alloying elements for the heat resistance of magnesium alloys

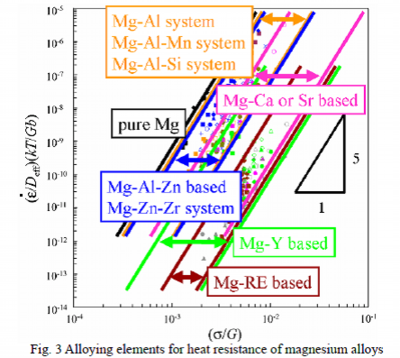
Many existing heat resistant magnesium alloys contain rare earth, RE.
⇒ Problems of RE and Y: Higher cost and localization in China
⇒ Preferable to choose extensively distributed elements, suggested Ca or Sr.
Published tensile test data of magnesium alloys at elevated temperature have been collected and the collected data are plotted in the relationship between stress and strain rate based on a constitutive equation to describe deformation at elevated temperature, to be discussed later, as shown in Fig. 3.
When referred to a certain strain rate, it can be stated that larger the stress to deform, higher the heat resistance. In other words, as the plot goes to the right side in the chart, the alloy is more heat-resistant.
In the existing heat-resistant magnesium alloys, Mg-Al-Mn system for the auto parts is major and rare earth elements such as La and Ce are indicated as effective additive elements. However, resources of these rare earth elements are confined and there are various uncertain factors in market. Therefore, it would be preferable to apply ubiquitous elements present widely on Earth. According to Figure 3, calcium, Ca, which is ubiquitous, or strontium, Sr, would have good heat-resistance-improvement effect comparable to the rare earth elements.
Determination of the basic alloy composition
・Mg-Al-Zn, AZ series, is widely used as structural material.
・Only ubiquitous elements, Ca and Sr, are added for alloying.
・No prior arts of this kind of magnesium alloy composition
↓
Selected Mg-Al-Zn-Ca-Sr alloys for development
Therefore, ubiquitous element of Ca and alkaline earth metal of Sr are selected for additive elements and the optimum formulation of the Mg-Al-Zn-based alloy has been studied, which is widely applied in die-casting due to good die-castablity.
Selected Ca is abundant locally. Sr is mainly supplied from China, but also has resources in Mexico.
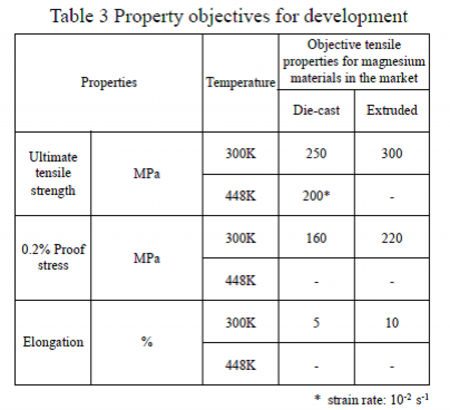
Target properties for development of the die-cast and extruded materials

・Reflecting requirements from market
・Tensile property objectives at ambient and elevated temperature: higher than AZ91 alloy, common die-cast material in the market
For the study of alloy compositions, target values of the tensile properties have been considered. The target values were optimized reflecting the needs of users for practical applications.
As shown in Table 3, the target values of the properties of die-cast material at ambient temperature are 250MPa or more of tensile strength, around 160MPa of 0.2% proof stress, comparable to that of commercially available AZ91 alloy, and 5% or more of elongation. These values are higher than tensile properties of die-cast material of widely used AZ91 alloy which has 230MPa of tensile strength, 160MPa of proof stress and 3% of elongation.
Microstructure and tensile properties at ambient temperature
・ Strengthening mechanism by grain size, d (Law of Hall-Petch)

σmg:Yield stress or 0.2% proof stress of magnesium alloys
σs:Yield stress or 0.2% proof stress of magnesium single crystal 8MPa
κ: Constant 220MPa・μm*1/2
・ Proof stress of magnesium alloys

Δσs: Incremental stress by solute strengthening
Δσp: Incremental stress by fine second phase particles, or other crystal particles in the crystal
It is known that determining factors of properties of magnesium alloys at ambient temperature are the crystal grain size, which follows the law of the Hall-Petch of Eq. 1, and strengthening by solid solution and the second phase particles of the added element as defined in Eq. 2. In order to achieve the target properties of the AZ91-CaSr alloy, which is the system we selected, synergy effect of the grain refinement and the strengthening by solid solution will be required.
Microstructure observation and grain size
Effects of addition of Ca and Sr on grain size of AZ91-CaSr based alloys

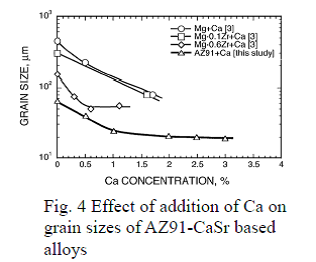

By grain refinement through addition of Ca and Sr to AZ91-CaSr based alloys, minimum grain size, around 20μm, is achieved as adding in combination with
・more than 1.0 mass % of Ca
and
・more than 0.5 mass % of Sr
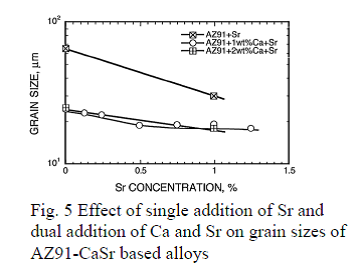
With regard to the effect of addition of Sr and Ca to AZ91 alloy, their influence toward the crystal grain size refinement was studied by adding Ca solely up to 3 mass% and Sr up to 1 mass% in addition to Ca. By adding Ca solely and Ca and Zr together to magnesium, grain refinement was observed as shown in Fig. 4, but the reached minimum grain size was about 60 ~ 80μm, which is comparable to the crystal grain size of AZ91 alloy of about 60 ~ 65μm. Addition of Ca to AZ91 refined the crystal grain size to approximately 20μm when more than 1mass% of Ca was added. As shown in Fig. 5, by adding Sr and Ca together, the crystal grain size was further refined and became less than 20μm when more than 0.5mass% of Sr was added. Consequently, it was found that the minimum grain size was achieved by combinational addition of 1.0 mass% of Ca or more and of more than 0.5 mass% of Sr.
Effects of insoluble metallic compounds
On properties of magnesium alloys

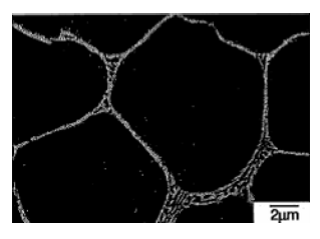
Fig. 6 Crystal structure of die-cast material of the heat-resistant Mg-Al-Ca magnesium alloy
Skeleton structure of metallic compounds in grain boundaries or in the vicinity of final solidification part
Fig. 6 shows a photograph of a typical die-cast magnesium alloy structure.
In this structure metallic compounds are present in the grain boundaries or in the vicinity of the last solidified part and the skeleton structure of the metallic compounds characterizes die-cast magnesium alloy.



Fig. 7 Representative microstructure of AZ91-CaSr based alloys
AZ91-1.0Ca0.5Sr alloy:More homogeneous structure ⇒ Effect on mechanical properties
As shown in Figure 7, four kinds of AZ91-CaSr alloy were prepared. Looking at the microstructure of these alloys, in any of the alloy, metallic compounds are continuously present in the grain boundaries or in the vicinity of the last solidified part, by which the skeleton structure is formed. It can be seen that the more Ca and Sr are added, the more area the characterizing skeleton structure covers. Lamellar structure is observed in the skeleton structure in larger amount of Ca and Sr added AZ91-2.0Ca-0.5Sr alloy. Only AZ91 alloy has a relatively coarse grain size of about 60 ~ 65μm and, as can be understood from the above indicated grain refinement effect of the combinational addition of Ca and Sr, AZ91-1.0Ca0.5Sr alloy has the minimum crystal grain size, dg, among prepared AZ91-CaSr alloys. Moreover, it is indicated that the combinational addition of Ca and Sr is also effective for homogenization of the skeleton structure. In particular, as mentioned referring to Fig. 5, it can be concluded that the combinational addition of Ca and Sr is very effective for the crystal grain refinement. This grain refinement relates to the mechanical properties.
Analysis results of the metallic compounds observed in AZ91 and AZ91-1.0Ca0.5Sr alloys

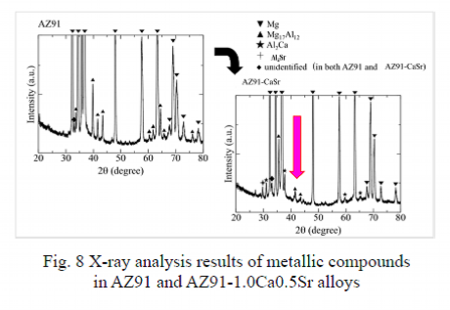

AZ91:Mg17Al12 only
AZ91-CaSr:Al2Ca, Al4Sr
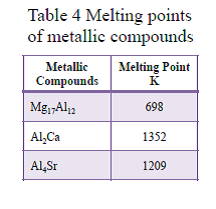
Metallic compounds with high melting points:Contribute to enhancement of heat resistance
X-ray analysis results of AZ91 and AZ91-1.0Ca0.5Sr alloy are shown in Fig. 8. Metallic compounds observed in AZ91 were only Mg17Al12 having low melting point of 698K. In contrast, when Ca and Sr are added, in addition to low melting point compound of Mg17Al12, high melting point compounds of Al2Ca of 1352K and Al4Sr of 1209K were observed. The melting points of the metallic compounds are listed in Table 4. In Ca and Sr added alloys, these high melting point compounds are to contribute to improvement of the heat resistance.
Tensile properties at ambient temperature

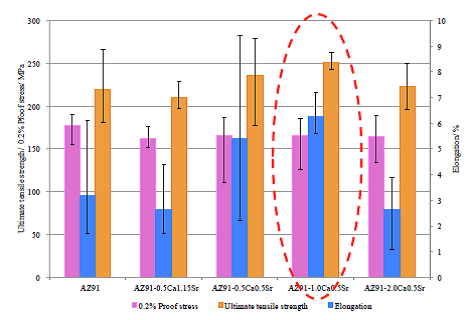
Fig. 9 Comparison of tensile properties of die-cast AZ91-CaSr based alloys at ambient temperature
AZ91-1.0Ca0.5Sr alloy has achieved property objectives at ambient temperature.
In tensile test results at ambient temperature as shown in Figure 9, the tensile strength of AZ91 alloy was approximately 220 MPa and Ca and Sr added alloys showed from 210 to 250 MPa which was comparable to AZ91 alloy. AZ91 showed around 180 MPa of proof stress which was higher than reported value of around 160 MPa. On the other hand, with regard to Ca and Sr added alloys, all of them had proof stress of around 165 MPa, which was comparable to yield strength of AZ91 alloy. The target values of this study, as indicated in Table 3, are 250 MPa or more of the tensile strength, around 160 MPa of proof stress of commercially available AZ91 alloy and 5% or more of elongation. The alloy which achieved the target values is only AZ91-1.0Ca0.5Sr alloy. Excellent mechanical properties at ambient temperature of AZ91-1.0Ca0.5Sr alloy might be derived from homogeneous and fine cast structure and fine grain size specific to this alloy. On the other hand, when compared to the AZ91 alloy prepared in this experiment, it is observed that addition of Ca and Sr together to AZ91 alloy tends to slightly decrease proof stress. However, it is found that the decrease of proof stress of these alloys are much smaller than that of the existing heat resistant magnesium alloys which usually is from 20 to 30 MPa and can be concluded that the heat resistant AZ91-CaSr alloys maintain the tensile strength of AZ91 at ambient temperature, which is characteristic of AZ91-CaSr alloy .
Tensile properties at elevated temperature
Table 5 Tensile test results of die-cast AZ91-CaSr based alloys at 448 K of temperature and 10-2 s-1 of strain velocity

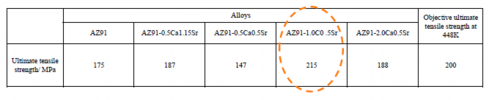
AZ91-1.0Ca0.5Sr alloy has achieved ultimate tensile strength objective at elevated temperature.
Constitutive equation to describe deformation behavior at elevated temperature


It has been examined if the target value of the mechanical properties at elevated temperature, specifically 200 MPa or more of the tensile strength at 448 K and at strain rate 10-2 s-1, can be achieved. The results are shown in Table 5. The alloy which passed the target values was AZ91-1.0Ca0.5Sr.With regard to the strength of AZ91-CaSr alloys at elevated temperatures, only AZ91-0.5Ca0.5Sr alloy, to which smallest total amount of Ca and Sr was added, had lower strength than AZ91. Strengths of other AZ91-CaSr alloys at elevated temperature were higher than the AZ91 alloy and it was observed that the strength at elevated temperature tends to depend on the volume fraction of the metallic compounds. This will be discussed later.Heat resistance of AZ91-CaSr alloy was analyzed using the constitutive equation to describe the deformation behavior at elevated temperature of Eq. 3.
Deformation mechanisms at elevated temperature analyzed by the constitutive equation
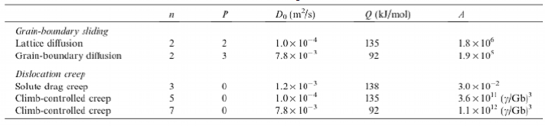
Table 6 Deformation mechanisms, indexes and constants in constitutive equation at elevated temperature

Constitutive equation of magnesium alloys deformed by dislocation creep at elevated temperature


The indexes and constants in Eq. 3 were reported by analyses of deformation mechanisms and are summarized in Table 6. Eq. 3-1 has been proposed for dislocation creep at elevated temperature incorporating the indexes in Table 6 into Eq. 3.It was reported that the stacking fault energy participated in the creep resistance of Mg-Y-Zn magnesium alloy by observation of the microstructure using TEM. It was also reported that in solid solution alloys, which deformation mechanism at elevated temperature was climb-controlled dislocation creep, the flow stress, which was stress required to initiate plastic deformation or to keep its deformation, depended on the stacking fault energy.
Analysis of determination factors of deformation behavior at elevated temperature by constitutive equation
![]()

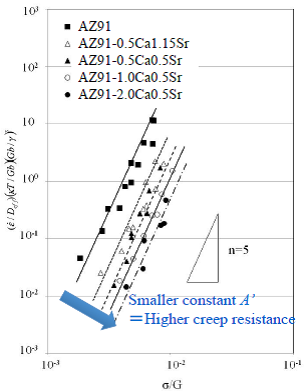


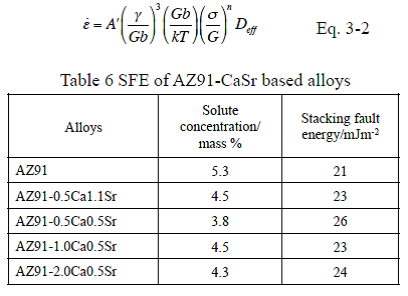
Therefore, the contribution of the stacking fault energy was analyzed using the constitutive equation to describe the deformation behavior at elevated temperature of Eq. 3-2 which included a term of the stacking fault energy, SFE. It is noted that the constitutive equation of Eq. 3-2 does not include a term of the crystal grain size d. This means that strengthening mechanism of the crystal grain refinement does not participate in the deformation of the magnesium alloy at elevated temperature. The results of analysis on solid solution concentration of added elements to magnesium showed that, in the AZ91-CaSr alloys of this study, the solid solution concentrations of Ca and Sr were small and Al was a major solute element, and therefore only Al has been taken into consideration as the solute element in further study. The SFE in this study were calculated referring to the studies by Uesugi et al. of Osaka Prefecture University, where they calculated by the first principles calculation in cases adding various solute elements to solvent magnesium. The SFE calculated for the aluminum solid solution concentrations are shown in Table 6. The difference in the SFE by the alloy composition is small and this is because Al solid solution concentrations of the alloys are almost the same. Normalized plots of the alloys using Eq. 3-2 are shown in Fig. 10. As plots of each alloy are on a straight line of the slope of 5, n of Eq. 3-2 is 5. When n is 5, it is reported that the deformation mechanism at elevated temperature is the dislocation creep as in Table 6. As the plots on straight lines and Eq. 3-2 shows that the flow stress in the dislocation creep relates to the SFE, it is obvious that the SFE participates in the deformation mechanism at elevated temperature of AZ91-CaSr alloys. However, despite the plots were normalized considering difference in SFE of each alloy, the line of an alloy moved toward higher stress by increasing amount of added Ca and Sr. This means that depending on increase of the added amount of Ca and Sr, heat resistance was improved and A’ of the constant in Eq 3-2, or the intercepts of the normalized plots in Fig. 10, decreased. This result will indicate that a factor other than the SFE or the characteristic microstructure, derived from the composition of the alloy or combinational addition of Ca and Sr, might participate in deformation behavior at elevated temperature.
Analysis of grain boundary coverage by the constitutive equation

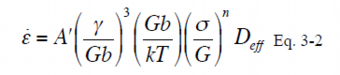
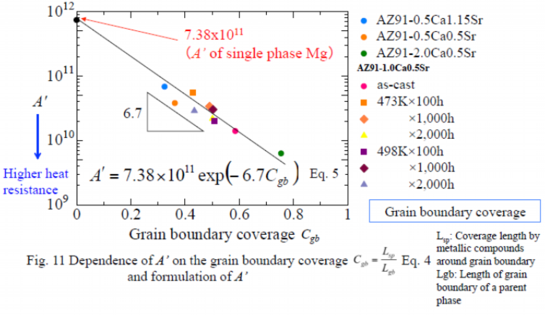

As one of factors affecting the deformation behavior of AZ91-CaSr alloys at elevated temperature, the grain boundary coverage of the metallic compounds had been studied. The grain boundary coverage is defined as Eq. 4. The grain boundary coverage, Cgb, was calculated referring to the results of the image analysis of the structure of each alloy and the calculated Cgb was plotted in relation to the constant A’ of Eq. 3-2 in Fig. 11. Fig. 11 shows that the larger the Cgb, the smaller the A’. As mentioned above that the higher the heat resistance, the smaller the A’, it can be concluded that the grain boundary coverage, Cgb, could be an indicator of the effect of the metallic compounds in the grain boundary. The relationship between the A’ and Cgb is formulated as Eq. 5.
Constitutive equation of AZ91-CaSr based alloys at elevated temperature considering effect of grain boundary coverage

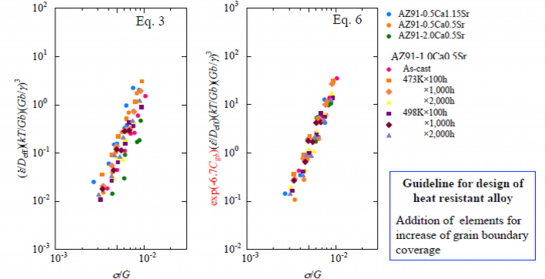

Fig. 12 Comparison of normalized plots of AZ91-CaSr alloys by the constitutive equations with and without a term of grain boundary coverage
Substituting Eq. 5 of A’ and Cgb into Eq. 3-2 including a term of the SFE, the constitutive equation of AZ91-CaSr alloys to describe deformation behavior at elevated temperature is eventually formulated into Eq. 6. The normalized plots of AZ91-CaSr alloys by Eq. 3-2 without the term of the grain boundary coverage and by Eq. 6 including the term of the grain boundary coverage are shown in Fig. 12. The plots dispersed in left chart in Fig. 11 plotted by Eq. 3-2 without the term of the grain boundary coverage. On the other hand plots concentrated and aligned on a straight line in the right chart plotted by Eq. 6 including the term of the grain boundary coverage. Thus the deformation of AZ91-CaSr alloys at elevated temperature is affected by the grain boundary coverage. From the above results, it will be summarized that the addition of elements, which extend the grain boundary coverage in the grain boundaries and in the vicinity of the last solidified part, is effective to improve the mechanical properties of the AZ91-CaSr alloys at elevated temperature in addition to the elements which decrease the stacking fault energies. From this summary a guideline for design of the AZ91-CaSr alloys with excellent mechanical properties at elevated temperature has been obtained: Addition of elements which decrease SFE and extend the grain boundary coverage is required.
Creep resistance of magnesium alloys at 448Kor 175 ℃

Creep:
A phenomenon of deformation, or increase of strain, of a material at elevated temperature in time course under a certain load or stress.
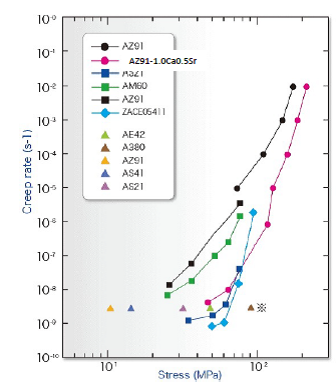
※:Creep resistant aluminum alloy A380.0(AlSi8Cu3Fe)for automotive engine parts
Fig. 13 Creep resistance of AZ91-1.0Ca0.5Sr alloy and existing heat resistant alloys
AZ91-1.0Ca0.5Sr alloy exceeded the target properties at ambient temperature and elevated temperature. The creep resistance of this alloy at 175 ℃ was compared with the existing heat-resistant magnesium alloys as in Fig. 13. It is confirmed that the developed AZ91-1.0Ca0.5Sr alloy has comparable creep resistance to or higher than the existing heat-resistant alloys and is demonstrated that the obtained guideline for design of the AZ91-CaSr alloys with excellent mechanical properties at elevated temperature is valid.
2. From die-cast materials to extruded or forged materials
Based on the findings obtained in die-cast material, formulation of alloys and deformation mechanisms of the extruded materials are studied.
Problems in extrusion of magnesium alloys
↓
Required compensation measures for extruded materials to improve the heat resistance

 Fig. 15 Texture of the die-cast and extruded materials
Fig. 15 Texture of the die-cast and extruded materialsFig. 16 Normalized plots by the constitutive equation on deformation at elevated temperature of pure Mg, AZ91 and die-cast and extruded, at extrusion ratio of 16, AZ01-1.0Ca0.5Sr alloy
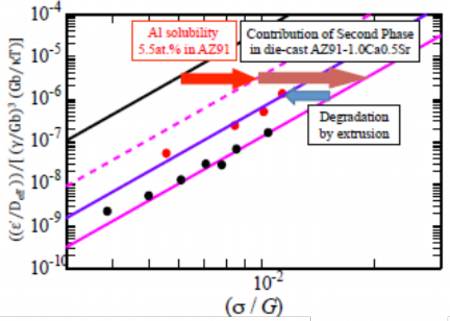
The skeleton structure of metallic compounds is observed in the die-cast material and this structure is one of dominant factors to improve of the heat resistance. However, this skeleton structure is broken into particulates by the extrusion processing as Fig. 15 and, therefore, contribution of the skeleton structure to the heat resistance cannot be expected in extruded materials. The metallographic controlling factors of the heat resistance of the extruded AZ91-1.0Ca0.5Sr alloy were analyzed applying the constitutive equation including the SFE to describe deformation behavior at elevated temperature. The results of analysis of samples extruded at extrusion ratio of 16 are shown in Fig. 16. As a typical aluminum solid solution concentration of AZ91-1.0Ca0.5Sr alloy, 6.3 mass% or 5.5 at. % was used for theoretical calculation in Fig. 16. Theoretically calculated dashed pink line of AZ91 alloy, which was mainly composed of magnesium and 6.3 mass% or 5.5 at. % of aluminum, was on right side to pure magnesium of black solid line and this shows improvement of the heat resistance, which is derived from the solid solution of aluminum.Ca and Sr added die-cast AZ91-1.0Ca0.5Sr alloy material of pink line was more heat resistant due to the second phase skeleton structure of the metallic compounds. However, the plots of the extruded AZ91-1.0Ca0.5Sr alloy material of purple solid line moved to left side to pink line of the die-cast material and located in between dashed pink line of the theoretically calculated AZ91 alloy containing solid solution of aluminum. These results tells that excellent heat resistance of the die-cast material is degenerated by extrusion, but it is suggested that metallographic factors of metallic compounds would improve the heat resistance in addition to the effect of solid solution of aluminum. Therefore, in order to improve the heat resistance of the extruded material, measures are required to compensate the destruction of the effective skeleton structure in the grain boundaries or in the vicinity of the last solidified part. In other words, while controlling the structure and texture of the metallic compounds, design of the alloy composition is required to exert effect of solid solution of aluminum to its best.
Measures to improve the heat resistance of the extruded material compensating disappearance of contribution of the grain boundary coverage by the metallic compounds
(2) Structural factors for improvement of heat resistance : Metallic compounds in grain boundaries⇒ Heat treatment to put metallic compounds in order

Factor 1. Average distance between metallic compounds λ
Factor 2. Threshold stress σ0
⇒Analysis by constitutive equation on deformation at elevated temperature
Threshold stress: Stress required to pass dislocations between particles
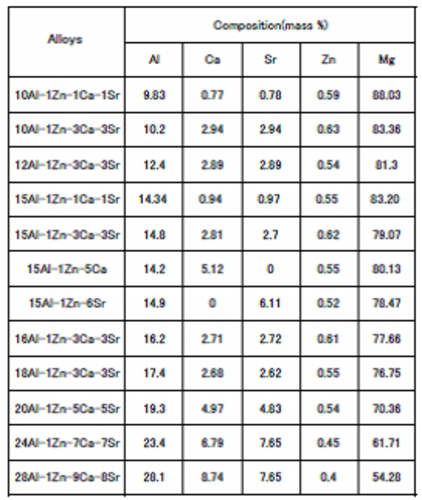
Table 7 Analysis results of composition of billets designed considering compensation measures of the disappearance of the contribution of the grain boundary coverage
Maximum dissolved Al concentration: 8.3 mass %
Heat treatment conditions


By heat treatment metallic compounds distributed homogeneously
↓
Heat treatment conditions after extrusion: at 673K for 48 h
15Al-1Zn-1Ca-1Sr and 15Al-1Zn-3Ca-3Sr alloys in Table 7 were designed for improvement of strength at elevated temperature by solid solution of aluminum. With regard to these two alloys heat treatment conditions after extrusion were examined to increase solid solution concentration. Temperature and time of the heat treatment were 673, 693 and 713 K or 400, 420 and 440 ℃ and 48 hours. After heat treatment samples were quenched in water. Figure 17 shows the changes in the microstructure by heat treatment. The microstructure was observed by the laser confocal microscope. Photographs of 15Al-1Zn-1Ca-1Sr show that metallic compounds were reduced by heat treatment at 673 K and this was because Mg17Al12 compounds were dissolved to solid-solution by the heat treatment. But metallic compounds were coarsened by the heat treatment at 693 K, although the volume was hardly changed. The solid solution concentration was almost saturated by heat treatment at 673 K and the metallic compounds coalesced and coarsened at higher temperatures. On the other hand, 15Al-1Zn-3Ca-3Sr alloy did not change the volume of the metallic compounds by heat treatment, but particles of the metallic compounds in crystal grains dispersed in grain boundaries by heat treatment at 673 K. By heat treatment at 693 K metallic compounds in grain boundaries began coarsening and substantial coarsening occurred by heat treatment at 723 K. It is obvious that metallic compounds uniformly distributed in the grain boundaries by heat treatment and the distributed metallic compounds coalesced and grew coarser by further heat treatment. From these results, the heat treatment conditions after extrusion has been decided as at 673 K and for 48 hours.
Analysis of strengthening mechanism at ambient temperature
Microstructure of the extruded alloys


After extrusion at an extrusion ratio of 16, the specimen was heat treated and the structure and texture was observed with the laser microscope as shown in Figure 18. Metallic compounds are dispersed by extrusion and coarser metallic compounds are observed in specimen including more elements.
Grain size

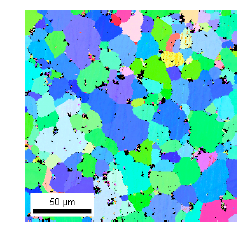
As Ca and Sr content increase, grain size refined under almost same solid solubility of Al.
For grain refinement Ca and Sr concentrations and the increase of metallic compounds would contribute.
Table 8 Grain sizes of extruded alloys

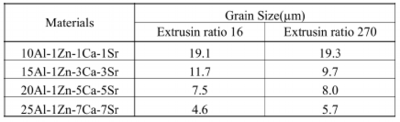

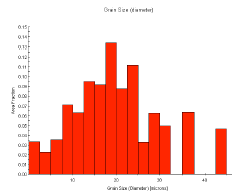
Fig. 19 Crystal orientation diagram and grain size distribution of 10Al-1Zn-1Ca-1Sr alloy
Crystal grain size was measured by crystal orientation analysis using the backscattered electron beam diffraction, EBSD, attached to the scanning electron microscope, SEM. The orientation diagram and crystal grain size distribution of 10Al-1Zn-1Ca-1Sr alloy measured by EBSD are shown in Fig. 19. Crystal grain sizes of the alloys extruded at extrusion ratio of 16 and 270 are listed in Table 8. The grain size became finer by addition of more Ca and Sr. Since solid solution concentrations of aluminum in alloys are almost the same, the grain refinement depends on increase of metallic compounds accompanied by increase of added volume of Ca and Sr.
Tensile test results at ambient temperature

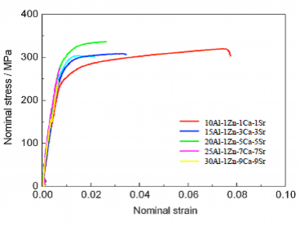
Fig. 20 Normal stress-strain curve of extruded alloys at extrusion ratio of 16
Table 9 Tensile test results at extrusion ratio of 16

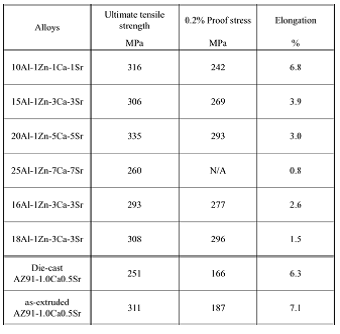
Nominal stress-strain curves of some of the extruded alloys at ambient temperature are shown in Fig. 20. Tensile test results at ambient temperature of extruded alloys at extrusion ratio of 16 are listed in Table 9. Proof stress increased and elongation decreased along with increase of amount of the added elements.
Analysis of strengthening factors at ambient temperature
Table 10 Strengthening factors at ambient temperature

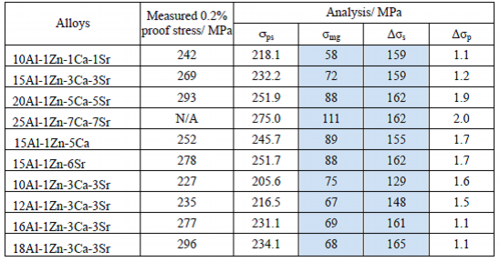

Measured 0.2% proof stress at ambient temperature and theoretically calculated results of deciding factors or terms in Eq. 2 are summarized in Table 10. Measured 0.2% proof stress and calculated strength of σps are closely related. The analysis revealed that the largest strengthening factor was solid solution of Δσs, effect of grain refinement of σmg was half of Δσs and contribution of Δσp by metallic compounds in grain boundaries was negligible. From this result, the design guideline of this study that aluminum should be dissolved in magnesium to solid solution up to its solubility limit has been demonstrated to be appropriate for improvement of strength at ambient temperature.
Analysis on the determination factors of the properties of the alloy at elevated temperature by the constitutive equation on deformation behavior
Tensile test results at elevated temperature

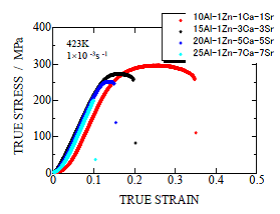
Fig. 21 True stress-strain curve of extrude alloys at extrusion ratio of 16
Table 11 Maximum tensile stress of the extruded materials at extrusion ratio of 16 and die-cast AZ91-1.0Ca0.5Sr alloy

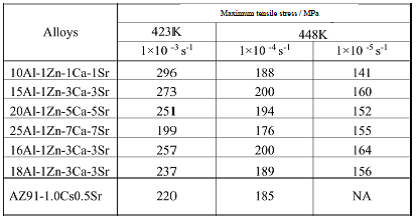
Property objectives: Those of die-cast AZ91-0.1Ca0.5Sr alloy
The true stress-strain curves of some of the extruded materials at elevated temperature are shown in Fig. 21. The maximum value of true stress of a curve is the maximum tensile stress. The results are summarized in Table 11. The maximum tensile stress of die-cast AZ91-1.0Ca0.5Sr, the target value, is also shown for comparison. Tested materials had higher strength at elevated temperature than the target values except 25Al-1Zn-7Ca-7Sr alloy fractured in brittle in the elastic region. Extruded materials at extrusion ratio of 16 have excellent mechanical properties at elevated temperature.
Analysis of a deciding factor at elevated temperature of the stacking fault energy


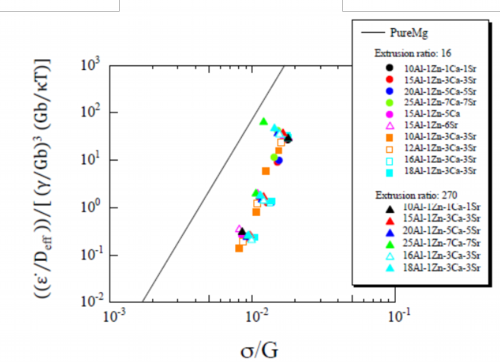
Fig. 22 Normalized plots of extruded materials at extrusion ratio of 16 and 270 by the constitutive equation including a term of stacking fault energy γ
Deformation behaviors of the extruded materials were examined using the constitutive equation including a term of stacking fault energy. Normalized plots of the extruded materials are shown in Fig. 22 where the constitutive equation of Eq. 3-2 including a term of stacking fault energy was applied. Plots of the materials, extruded at extrusion ratio of 16 and 270, distributed in higher heat resistance area from the line of pure magnesium and they were almost on a single straight line. The constant A’ was decided as Eq. 7. However, deviation of the plots from the straight line was observed on data in the lower stress.
Comparison of experimental data and theoretically calculated analysis results on stacking fault energy of solid-solution aluminum

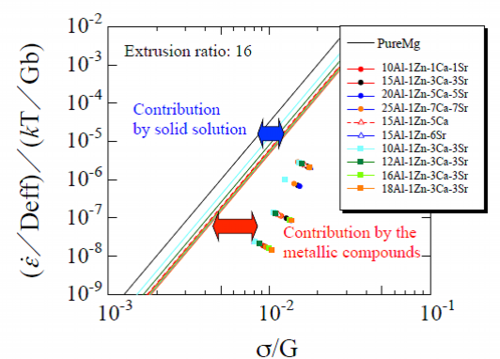
Fig. 23 Normalized plots of pure magnesium, analysis results on contribution of stacking fault energy of aluminum solid-solution and experimental data of extruded materials at extrusion ratio of 16
Figure 23 shows the experimental data and analysis results obtained by calculating the contribution of stacking fault energy of the solid solution of aluminum. Black solid line is of pure magnesium which was theoretically calculated by the constitutive equation as before and other lines are of the calculated analysis results of extruded materials by the constitutive equation including a term of stacking fault energy. As Fig. 23 shows, the deviation of the line of analysis results from the pure magnesium of black line is derived from the contribution of the reduced stacking fault energy by the solid solution of aluminum. The deviations of plots of the experimental data from the straight lines of the analysis results of the respective materials are considered to be the effect of the metallic compounds in grain boundaries.
Analysis results on average distance λ between metallic compounds

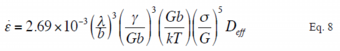
λ: Average distance between metallic compounds


Fig. 24 Normalized plots of the extruded materials at extrusion ratio of 16 and 270 by the constitutive equation including λ at elevated temperature
Concerning effect of the compounds in grain boundaries to improve heat resistance, effects of size of sub-grains, distance between particles λ and volume fraction Vf of compounds have been reported on SiC reinforced aluminum matrix compound materials. On the basis of these prior studies the deviation of experimental results from theoretical analysis, as shown in Fig. 23, was analyzed applying the constitutive equation in which the average distance λ between the metallic compounds was added to Eq. 3-2. λ was quantified from photographic observation of each metallographic structure and used in the analysis. The normalized plots of the extruded materials are shown in Fig. 24 using the analysis results of λ and tensile test results. Plots were distributed in the vicinity of the straight line of pure magnesium. This result indicates that the average distance λ between metallic compounds is a factor in deformation of the extruded materials at elevated temperature and that the metallic compounds in the grain boundaries affect deformation. In Fig. 24 the deviation of plots from the straight line in lower stress was also observed.
Analysis by constitutive equation including threshold stress

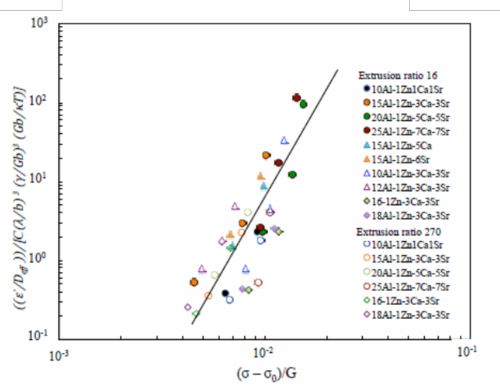

Fig. 25 Normalized plots by an experimental constitutive equation including average distance between metallic compounds λ and threshold stress σ0 of extruded materials
Extruded materials of this study, as showed by structural photographs in Fig. 18, include metallic compounds in grain boundaries as they were designed in accordance with the guideline for design of the alloy described above. As these metallic compounds present in the grain boundaries may govern the deformation behavior at elevated temperature and, in particular, suppress the movement of dislocation at the grain boundaries, the metallic compounds will relate to the threshold stress. The threshold stress was obtained through the procedure as the threshold stress σ0 was introduced in the constitutive equation of Eq. 8, then measured tensile data were plotted using said constitutive equation and the intercept of the plot at σ = 0 of the threshold stress σ0 was calculated according to the calculation method of the threshold stress. The normalized plots of said constitutive equation including terms of the average distance of metallic compounds λ and the threshold stress σ0 are shown in Fig. 25. As the plots were distributed in the vicinity of a straight line, it is revealed that the threshold stress σ0 is one of the governing factors of the deformation behavior at elevated temperature or the heat resistance. From the straight line in Fig. 25, experimental constitutive equation Eq. 9 has been obtained.
Relationship between average distance between the metallic compounds λ, threshold stress σ0 and creep resistance
Table 12 Creep elongation of extruded

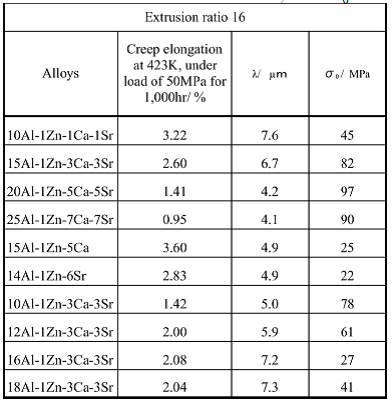
Concerning the extruded material of the this study, the relationship was studied between average distance between the metallic compounds λ, threshold stress σ0 and creep resistance, which was expressed by the creep elongation loaded with 50MPa at 423K for 1,000 hours. Test results are summarized in Table 12. Four alloys of 10Al-1Zn-1Ca-1Sr, 15Al-1Zn-3Ca-3Sr, 20Al-1Zn-5Ca-5Sr and 25Al-1Zn-7Ca-7Sr, in which residual aluminum contents were designed to be equal to the solid solubility limit, have larger σ0 and smaller creep elongation when λ are smaller. In these alloys, more Ca and Sr were added in proportion to the amount of aluminum, so the added aluminum formed metallic compounds such as Al2Ca, Al4Sr and increased volume fraction of the metallic compounds in grain boundaries in accordance with increase of aluminum content. This shows that the increase of metallic compounds in grain boundaries makes the average distance between the metallic compounds of λ smaller and threshold stress of σ0 larger. This result clearly indicates that the metallic compounds having high melting points in the grain boundaries suppress grain boundary diffusion of dislocation such as the grain boundary migration and grain boundary sliding at low strain rate. Therefore, in design of composition and control of heat resistance of Mg-Al-Zn-Ca-Sr-based magnesium alloys, it will be concluded that it is necessary to consider formation of the metallic compounds in the grain boundaries.
Summary
(1)Effects of alloy composition and microstructure toward tensile properties of heat resistant Mg-Al-Ca-Sr alloys were systematically studied and the guideline for design was obtained as to increase solid solution concentration of aluminum to its solubility
limit.
(2)Dominant factors to improveAZ91-CaSr alloys were analyzed and found that they were:
– Decrease of the stacking fault energy by solid solution of aluminum
– Increase of the grain boundary coverage
These are the guideline for design of composition of the heat resistantAZ91-CaSr alloys for die-casting.
(3)Obtained knowledge on die-cast materials was extended to design of composition of
Mg-Al-Ca-Sr alloys for extruded materials having balanced tensile properties at ambient and elevated temperature.
Strengthening mechanisms at ambient temperature are:
– Grain refinement
– Solid solution
Factors to improve heat resistance are:
Accompanied by the increase of grain boundary coverage of metallic compounds,
– Substantial decrease of λ
– Increase ofσ0